随便写写

龙书的P431中有一个quicksort的不含嵌套函数及高阶函数的例子，我实现的时候居然错了，真的太菜了。虽然整体的思想都是让问题退化为解决枢轴两边的快排问题，但是在处理细节上是不同的。虽然基础，但是好记性不如烂笔头，还是硬着头皮写下吧>_<

方法一

public class Qs {
	private int[] numbers;
	private int number;

	public void sort(int[] values) {
		if (values == null || values.length < 2) {
			return;
		}
		this.numbers = values;
		number = values.length;
		quicksort(0, number - 1);
	}

	int partition(int low, int high) {
		int pivotKey = numbers[low];
		while (low <= high) {
			while (numbers[low] < pivotKey) {
				low++;
			}
			while (numbers[high] > pivotKey) {
				high--;
			}
			if (low <= high) {
				exchange(low, high);
				low++;
				high--;
			}
		}
		return low;
	}

	private void quicksort(int low, int high) {
		int i = partition(low, high);
		if (low < i - 1) {
			quicksort(low, i - 1);
		}
		if (high > i) {
			quicksort(i, high);
		}
	}

	private void exchange(int i, int j) {
		int temp = numbers[i];
		numbers[i] = numbers[j];
		numbers[j] = temp;
	}

	public static void main(String[] args) {
		int[] arr = { -4, 4, 3, -1, 2, 1, -3, -2, 0 };
		Qs qs = new Qs();
		qs.sort(arr);
		for (int ele : arr)
			System.out.print(ele + " ");
	}
}

方法二（修改方法一中的partition和quicksort）

int partition(int low, int high) {
		int pivotKey = numbers[low];
		while (low < high) {
			while (low < high && numbers[high] >= pivotKey)
				high--;
			exchange(low, high);
			while (low < high && numbers[low] <= pivotKey)
				low++;
			exchange(low, high);
		}
		return low;
	}

	private void quicksort(int low, int high) {
		if (low < high) {
			int pivotKey = partition(low, high);
			quicksort(low, pivotKey - 1);
			quicksort(pivotKey + 1, high);
		}
	}

注意细节即可，这里就不演示了。想了解一下细节的话可以加断点细细分析；或者加些aspect的信息来看一下。下面是直接用aspectj插入的一些信息：

public aspect QsAspectj {
	
	private int callDepth = -1;
	
	pointcut MethodInfo(int low,int high):call (* *(..))&&this(Qs)&&args(low,high);
	before(int low,int high):MethodInfo(low,high){
		callDepth++;
		System.out.print(callDepth);
		for(int i = 0; i< callDepth;i++)
			System.out.print("   ");
		System.out.println(thisJoinPointStaticPart.getSignature().getName()+"("+low+", "+high+")");
	}
	after(int low,int high):MethodInfo(low,high){
		System.out.print(callDepth);
		for(int i = 0; i< callDepth;i++)
			System.out.print("   ");
		System.out.println(thisJoinPointStaticPart.getSignature().getName()+"("+low+", "+high+")");
		callDepth--;
	}
	
	pointcut sortInfo():call(public void sort(int[]))&&within(Qs);
	Object around():sortInfo(){
		long begin = System.nanoTime();
		Object result = proceed();
		long end = System.nanoTime();
		System.out.println("total time: "+(end-begin));
		return result;
	}
	before():sortInfo(){
		System.out.println("*** "+thisJoinPointStaticPart.getSignature().getName()+" ***");
	}
	after():sortInfo(){
		System.out.println("*** "+thisJoinPointStaticPart.getSignature().getName()+" ***");
	}
}

class Quicksort {
  def sort(a: Array[Int]): Array[Int] =
    if (a.length < 2) a
    else {
      val pivot = a(a.length / 2)
      sort(a filter (pivot >)) ++ (a filter (pivot ==)) ++
        sort(a filter (pivot <))
    }  
}

object Quicksort extends Application {
  val qs = new Quicksort
  val a = Array(-4, 4, 3, -1, 2, 1, -3, -2, 0)
//  val start = System.nanoTime()
  val sorted = qs.sort(a)
//  val end = System.nanoTime()
//  println("total time: " + (end - start))
  sorted.foreach(n => (print(n), print(" ")))
}

貌似这样的做法不怎么高效（不妨看看运行时间），但鉴于我的scala还只勉强达到入门级，如何改进还得以后再说。

1. CFG(contex free grammer而非control flow graph)比regex牛逼些：regex能生成的language是CFG能生成的language的(真)子集。NFA向CFG的规约可以按照下面的步骤：
   1. 为每个NFA中的状态$i$生成一个nonterminal $A_i$
   2. 若对于输入$i$有从$i$到$j$的状态转移，添加production $A_i\rightarrow aA_j$（若$a=\varepsilon$则添加production $A_i\rightarrow A_j$）
   3. 若$i$为初始态，令$A_i$为grammer的start symbol；若$i$为终态添加$A_i\rightarrow\varepsilon$
2. regex（或FA）不能表达全部CFG能够表达的语法（“有限状态机不会数数”）。比如$L= \{a^nb^n|n\ge1\}$，可以用反证法证明它不能用有限状态机表述。
3. 解释性语言天生就比编译型语言跨平台；它们至多只需要有统一的解释器罢了。Java就是这样一个另类（半编译半解释），而且还假装把这个解释器用的虚拟机做得像真的机器似的。所以虚拟化很重要啊，当解决不了问题或解决问题的方法不够妥当时，考虑加一个中间层的确有帮助。
4. derivation和parser tree之间存在$1\rightarrow n$的关系，因为derivation是整个过程而parser tree是最终的结果而已；不过如果限定某种派生的准则（如leftmost/rightmost）两者就一一对应了。下面是两种不同的派生：

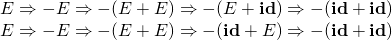
5. parser tree是具体的语法树，其内部节点必然是非终结的（nonterminal，表示规则名），关注的是树节点的类型；syntax tree又称抽象语法树（AST），其内部节点仅仅表示程序结构。（$S_{nonterminal}\varsubsetneqq S_{programming constructs}$）。parser tree比较严格，比如9-5+2中的9一定得画成像$number\rightarrow 9$这样的形式。大多数情况下，parse tree不如AST合适，但parser容易自动生成parse tree。
6. JavaCC是词法分析器和语法生成器，用的是top-down的方式生成LL(k)语法，所以left recursive不能用。Lex是词法扫描器，Yacc是语法分析的，bottom-up。其中概念较多，以后单独对这部分内容作笔记。

不懂编译原理没法在实验室混啊，开始写些流水帐笔记，目的只是为了重新补上这一课；仅代表个人知识水平，万不可因此而怀疑我的师兄和同学们>_<。参考教材Compilers: Principles, Techniques, and Tools（龙书）。

-------------------------------------------------------

1. Lexical analyzer生成token给parser用，分析过程还得和symbol table交互；在分析过程中需要干掉comments和whitespace（whitespace指的是blank，newline和tab或其他用于分隔token的东东，而不仅仅是空格）。

2. token的样子是(token-name,attribute-value)，其中attribute-value对保留字、操作符是不需要的；对于token-name是id的情况，attribute-value一般是指向其所在符号表中的项的pointer；对于数字这样的输入，可以让attribute-value表示对应的值，但实际一般还是用一个pointer指向表示它的字符串。

3. lexeme是源程序中的具体字符序列；pattern是对模式的描述；token可看成对lexeme的泛化（类似于OO中的class）

4. 识别lexeme时需要向前看几个字符（比如看到<有可能是<=或<）；同时为减少io读取次数，使用双buffer。

5. 每次需检查buffer终点并确定读入的字符是什么，为求统一使用sentinel（输入中不会出现的字符，如eof）

6. DFA$\subset$NFA，DFA初初始态不可为$\varepsilon$且每一个状态只有一个出边；DFA和NFA等价，可以类比群中的加法和乘法；其中DFA中的一个状态可看成NFA中的状态组成的集合（subset construction）。